Advancing the Water Shader

One of my first shaders was the “water-coloured” water shader. The aesthetic was to fit liquid in a paper world, paint/water-coloured seemed quite fitting. While the shader has changed over time the basics remained, a gradient + noise + remap, now we have fancier things like specular shading and normal maps.

Original water


New water

In other projects I had modelled the water mesh in a 3D modelling program but to make Origami Ninja Star a more dynamic solution was needed. I decided to use an in-engine tool to create rivers through Bezier curves. Specifically cubic Bezier curves, here is a link to a great primer, the evaluation function is fairly simple.

float3 Bezier(float3 p0, float3 p1, floa3 p2, float3 p3, float t):
  float t2 = t * t;
  float t3 = t2 * t;
  float mt = 1-t;
  float mt2 = mt * mt;
  float mt3 = mt2 * mt;
  return p0*mt3 + 3*p1*mt2*t + 3*p2*mt*t2 + p3*t3;

I found a similar free road building tool with curve editor capabilities and heavily modified it to instead create rivers. I also added in additional features such as water thickness, varying width, and different/multiple materials.

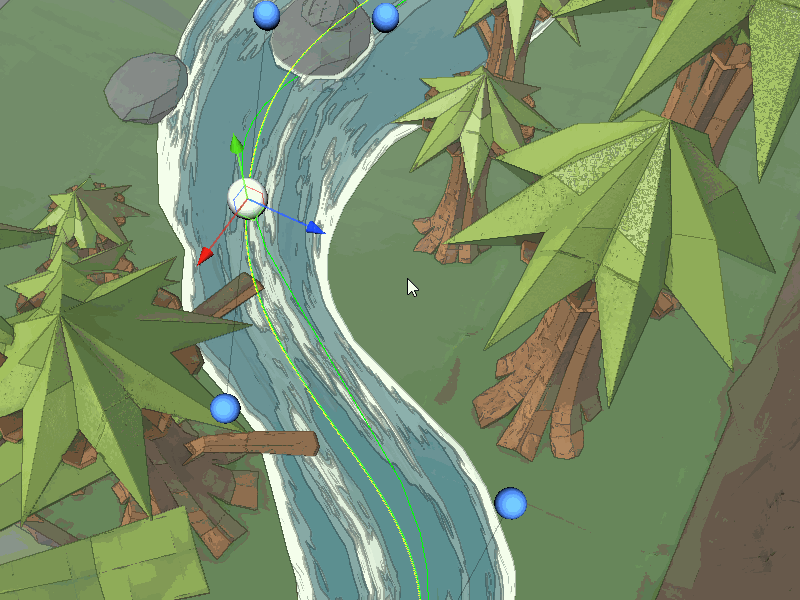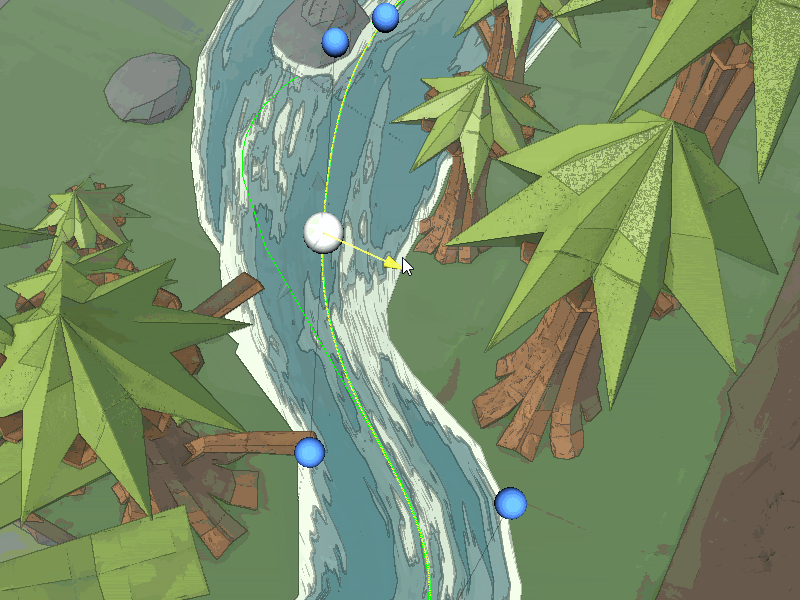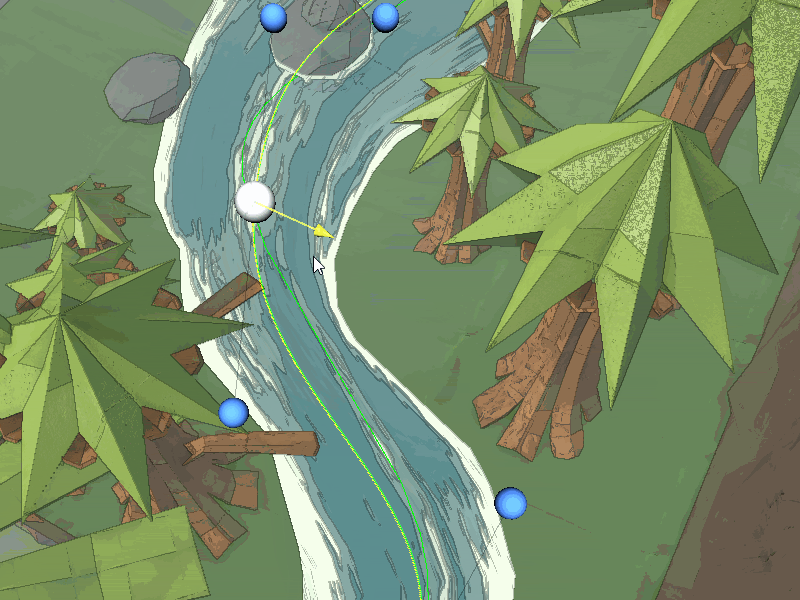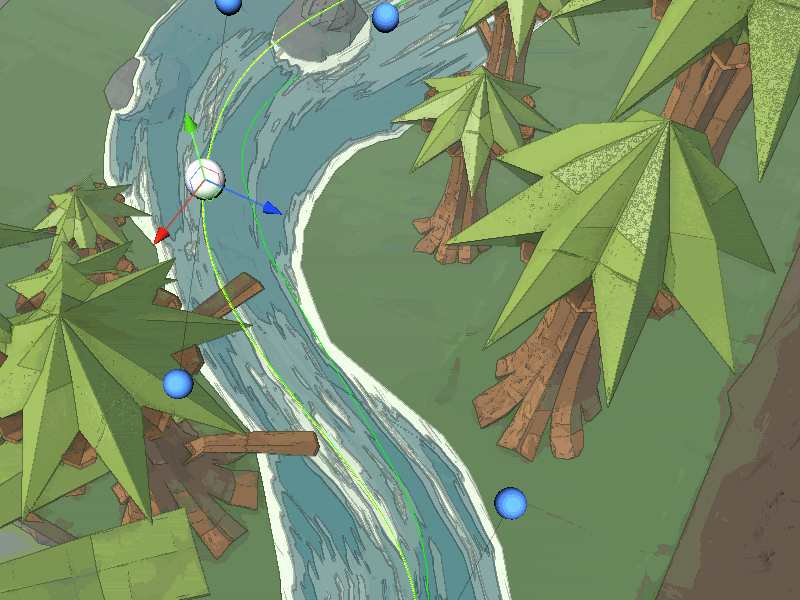
Another issue was water detail was lacking with this method due to the lack of polys. This lead me to everyone’s favourite water feature tessellation. Implementing tessellation in URP was surprisingly straight forward and extremely messy but it adds much greater visual fidelity to the water, especially with waves.

Now finally the purpose of all these components is to make the water physical. In Origami Ninja Star you can surf the water and waves. For waves a more realistic approach is to use Gerstner waves, which look great but I feel are a bit excessive for my more stylised game. So instead I’m using a simple Sin wave + simplex noise to add visual variation. This is more performant and easy to use later on.

No tessellation wave

With tessellation wave

Thanks to our tessellation the waves will always have excellent detail with the player interacts with them. This means the collisions will always look quite accurate. To perform these on the CPU side we just need to sync the data from the shader to the collision function, which again is just a Sin wave. Some additional information required for a robust water collision system, we need to also calculate the normals. Thanks to our simple wave equation finding the derivative for the wave is simple, just Cos and some basic transformations.

   // x is our distance along the sin wave (sin(x))
   float cosDx = 0.5f * heightMultiplier * waveFrequency * Mathf.Cos(x);
   Vector2 normal2D = new Vector2(-cosDx / Mathf.Sqrt(cosDx * cosDx + 1.0f),
                                   1.0f / Mathf.Sqrt(cosDx * cosDx + 1.0f));
   Vector3 normal = normal2D.x * transform.forward + normal2D.y * transform.up;
   return normal;

Now we can use the normal in physics calculations.

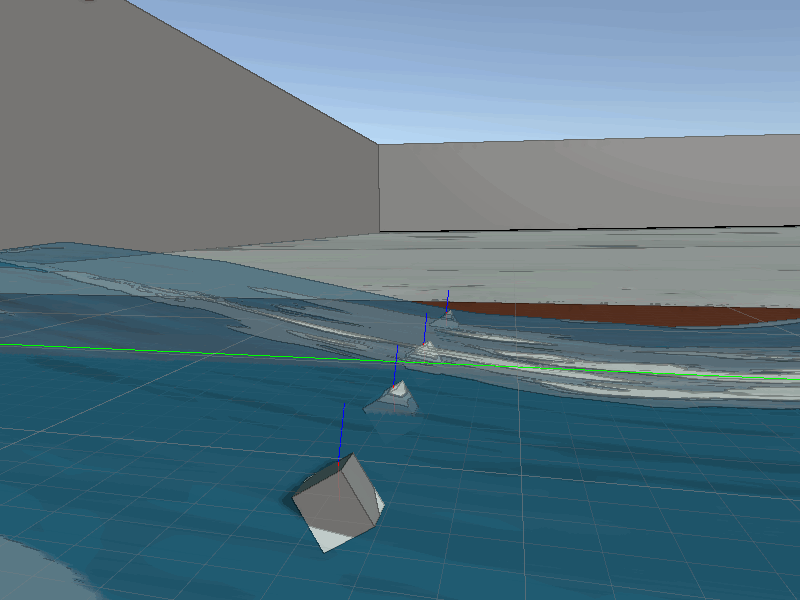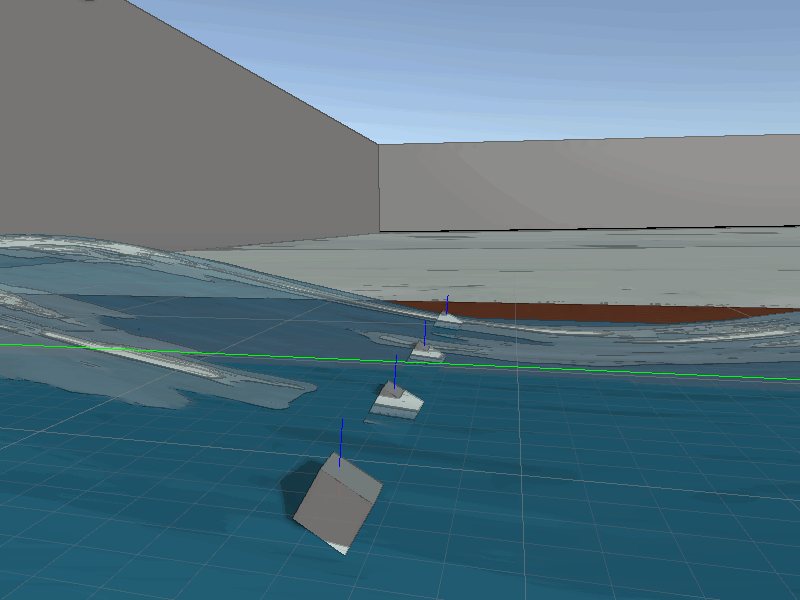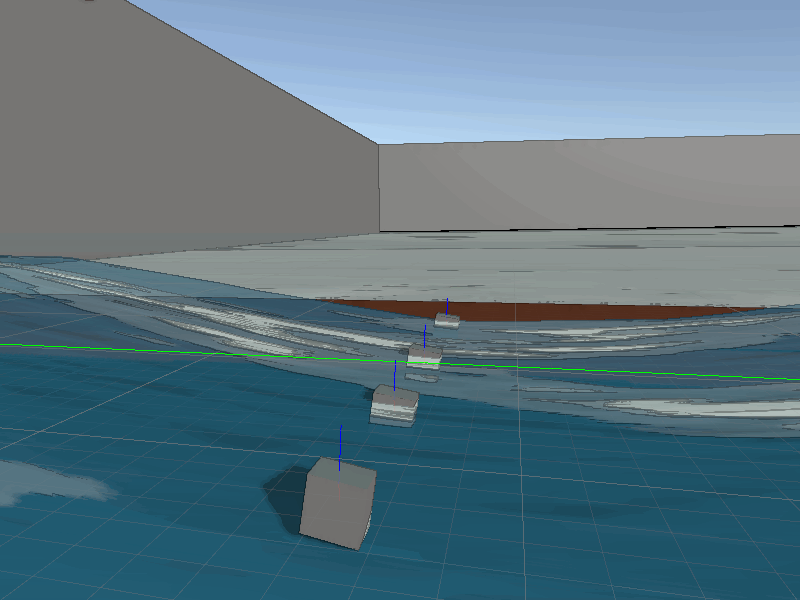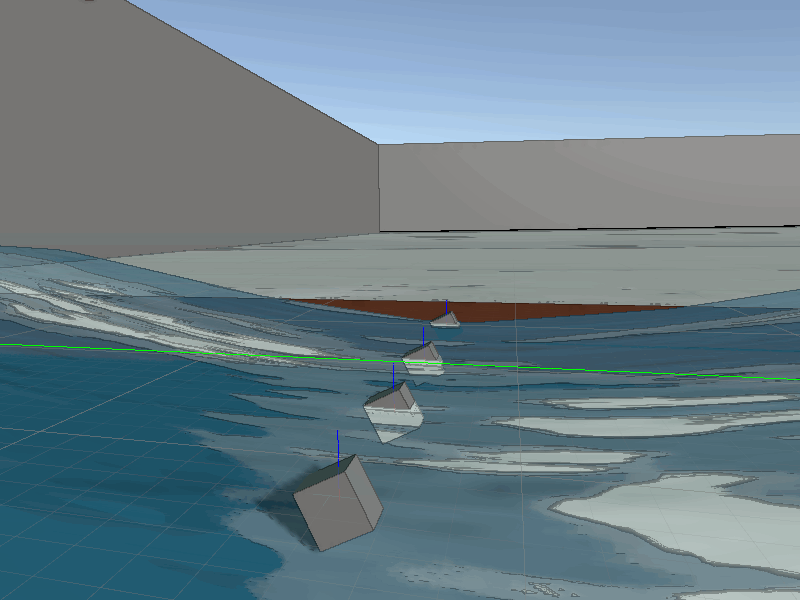
Surface point (red), Surface normal (blue)

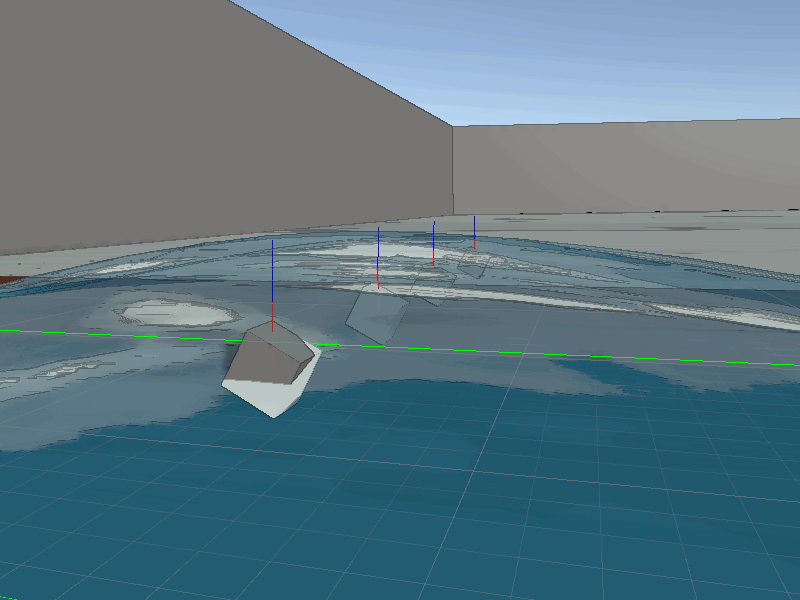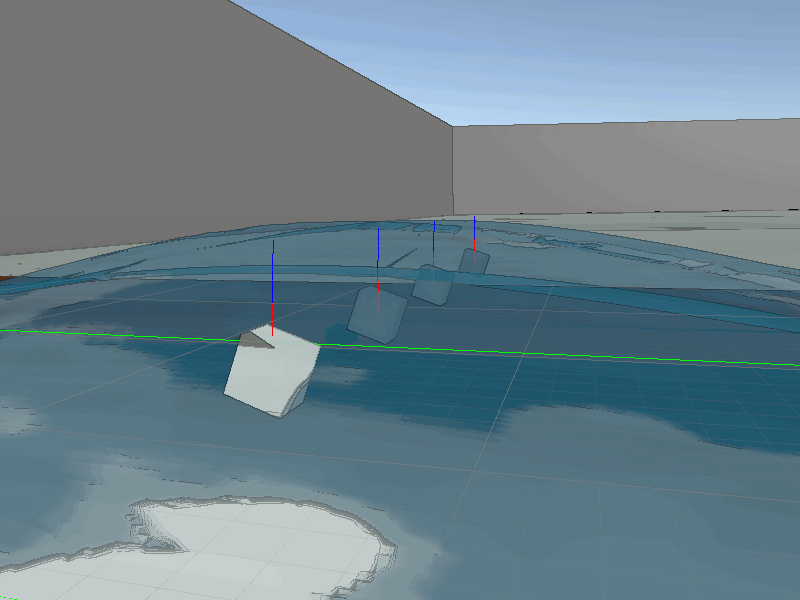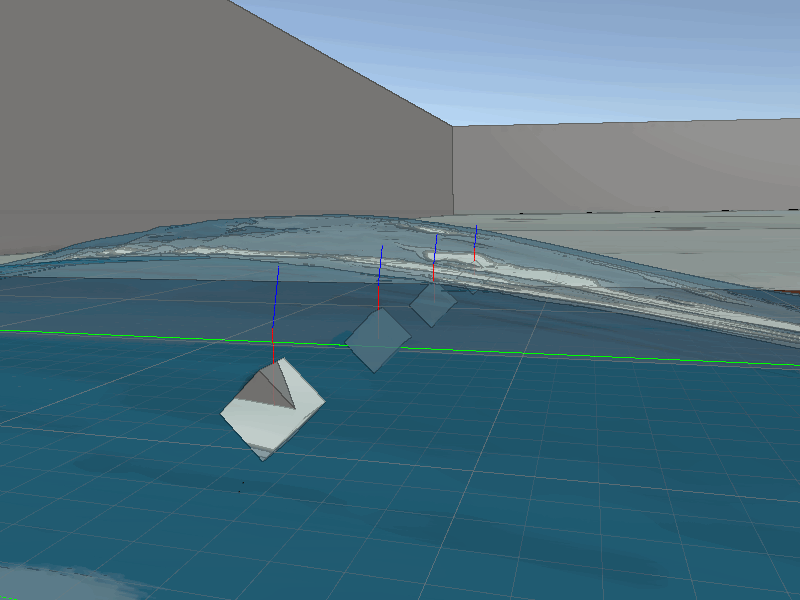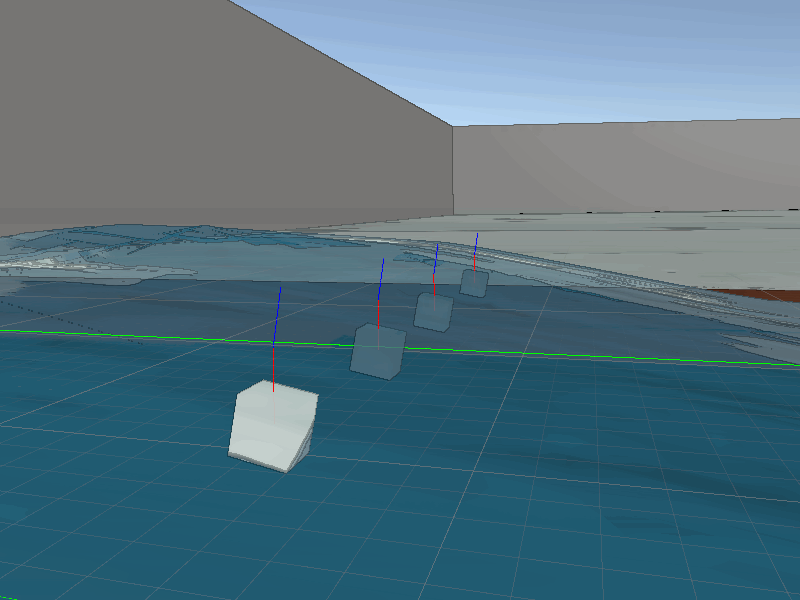
With moving rigid-bodies